Positional Encoding

Sinusoidal

Attention is All You Need

$$\begin{array}{rl}PE(pos,2i)& =\sin (pos/{10000}^{2i/d_{\text{model}}})\\ PE(pos,2i+1)& =\cos (pos/{10000}^{2i/d_{\text{model}}})\end{array}$$

Then add it to the input vectors.

NoPE

Length Generalization of Causal Transformers without Position Encoding

No positional encoding.

Additive

ALiBi

Train Short, Test Long: Attention with Linear Biases Enables Input Length Extrapolation

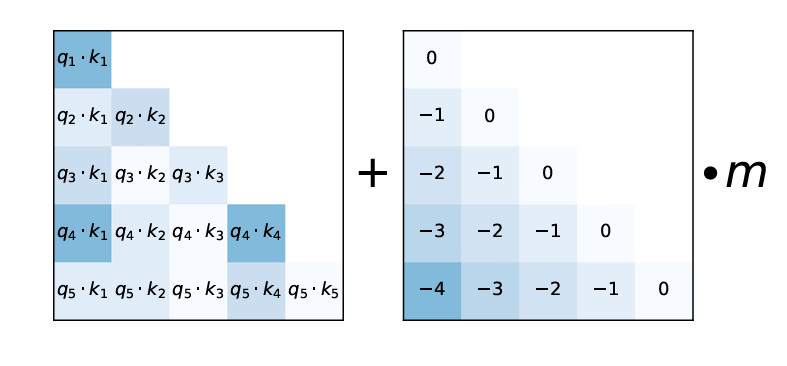
• Original attention score: $\mathrm{softmax}({\mathbf{\text{q}}}_i{\mathbf{\text{K}}}^T)$
• With AliBi: $\mathrm{softmax}({\mathbf{\text{q}}}_i{\mathbf{\text{K}}}^T+m\cdot [-(i-1),\dots ,-2,-1,0])$
• $m$ is a const head-specific scalar: $2^{\frac{-8}{n}}$ for the $n$th head.
• No positional encoding.

T5's RPE

Exploring the Limits of Transfer Learning with a Unified Text-to-Text Transformer

$${\mathbf{\text{B}}}_{i,j}=r_{\min (i-j,K)}$$

• $K$ is hyper-parameter.
• $r_i$ are learnable scalars.

Kerpel

KERPLE: Kernelized Relative Positional Embedding for Length Extrapolation

$${\mathbf{\text{B}}}_{i,j}=-r_1\log (1+r_2|i-j|)$$

Sandwich

Dissecting Transformer Length Extrapolation via the Lens of Receptive Field Analysis

$${\mathbf{\text{B}}}_{i,j}=r_1\sum _{k=1}^{r_2}\cos (\frac{i-j}{{10000}^{k/d^{\prime }}})$$

FIRE

Functional Interpolation for Relative Positions Improves Long Context Transformers

${\mathbf{\text{B}}}_{i,j}=f_{\theta }\left(\frac{\psi (i-j)}{\psi (\max \{L,i\})}\right)$

• $f_{\theta }:\mathbb{R}\to \mathbb{R}$ is MLP.
• $\varphi :\mathbb{N}\to {\mathbb{R}}_{+}$ is monotonically increasing (e.g. $\varphi (x)=\log (cx+1)$).
• $L>0$ is a learnable scalar.

CaPE

CAPE: Context-Adaptive Positional Encoding for Length Extrapolation

• ${\mathbf{\text{A}}}_{\text{CAPE}}(\mathbf{\text{X}})=\mathbf{\text{X}}{\mathbf{\text{W}}}_Q(\mathbf{\text{X}}{\mathbf{\text{W}}}_K{)}^{\mathrm{\top }}+f(\mathbf{\text{X}}{\mathbf{\text{W}}}_Q(\mathbf{\text{X}}{\mathbf{\text{W}}}_K{)}^{\mathrm{\top }},\mathbf{\text{B}})$
• $f$ is a two-layer LeakyReLU neural network.
• $\mathbf{B}$ is positional bias matrices (e.g. ALiBi and FIRE).

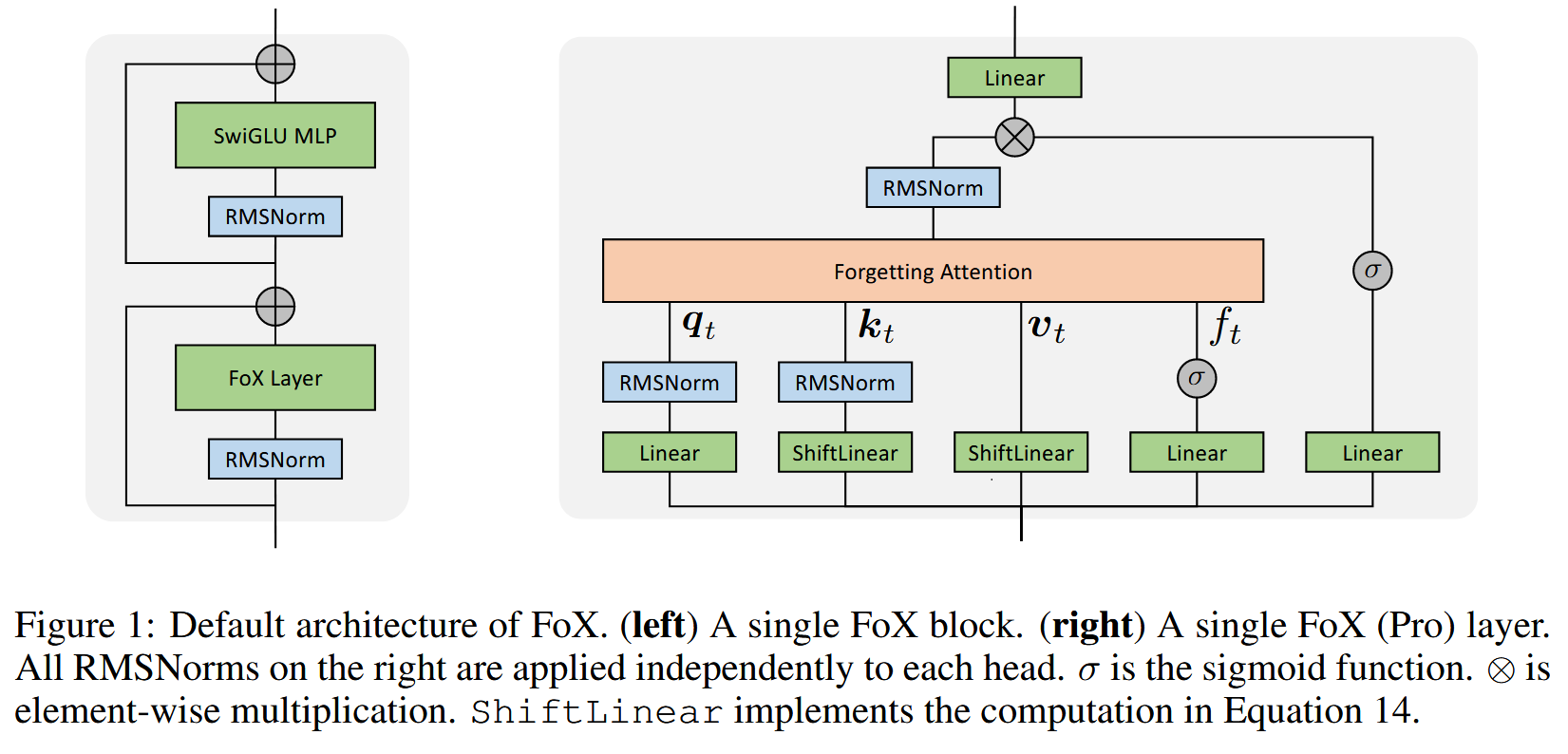
FoX

Forgetting Transformer: Softmax Attention with a Forget Gate

• Dynamic down-weighting of past information.
• No need of position embeddings.
• Compatible with FlashAttention.

1. Scalar Forget Gate

   $$f_t=\sigma (w_f^{\mathrm{\top }}{x}_t+b_f)$$

   Where $w_f$ and $b_f$ are learnable and per-head (for multiple head attention).

2. Cumulative Forget Factor

   $$\begin{array}{rl}& F_{ij}=\prod _{l=j+1}^i{f}_l(1\text{ if }i=j)\\ & B_{ij}=\log F_{ij}=\sum _{l=j+1}^i\log f_l\end{array}$$

FoX (Pro)

CoPE

Contextual Position Encoding: Learning to Count What's Important

• Dynamically decide which tokens should be counted based on the context.
• More flexible position addressing (e.g. i-th specific word, noun, or sentence).

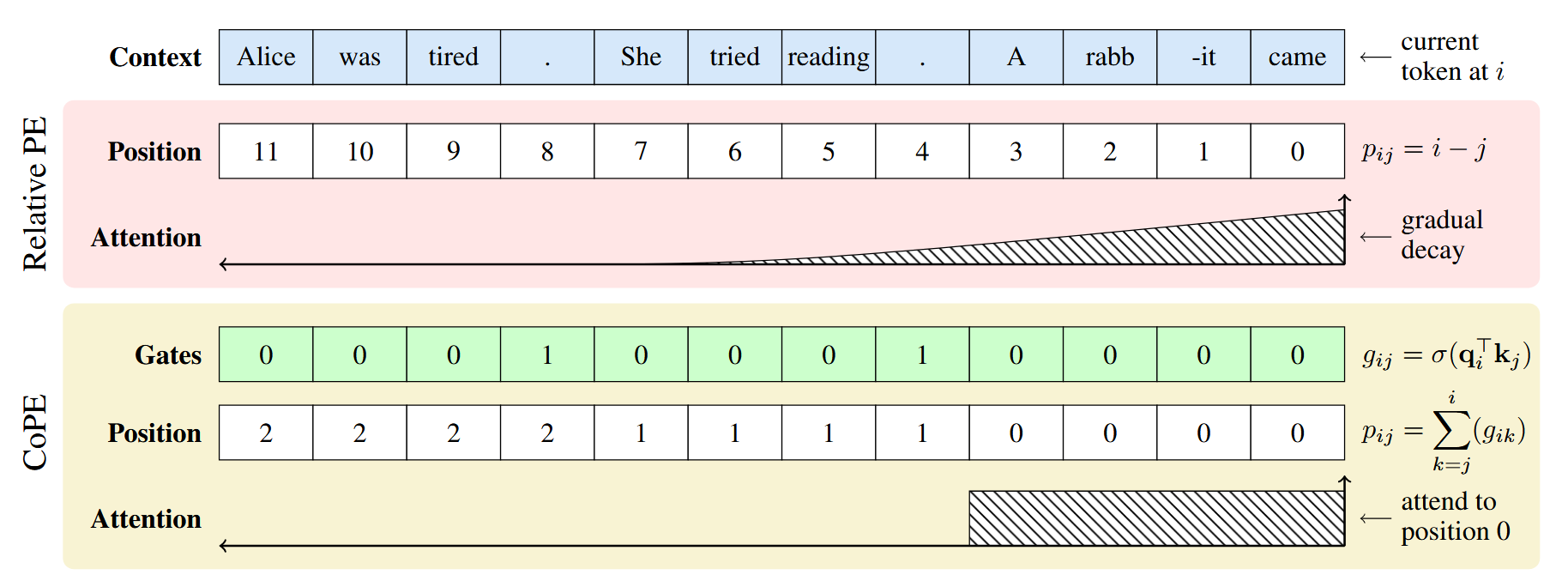
1. Gate Computation

   $$g_{ij}=\sigma \left(q_i^T{k}_j\right)$$

2. Contextual Position Calculation

   $$p_{ij}=\sum _{k=j}^i{g}_{ik}$$

3. Position Embedding Interpolation

   • Because $p_{ij}$ may be a fraction, interpolation is used to compute the embedding vector.
   • For each integer position, a learnable embedding vector $e[p]$ is used.
   • For decimal position: $e\left[p_{ij}\right]=(p_{ij}-\lfloor p_{ij}\rfloor )e\left[\left[p_{ij}\right]\right]+(1-p_{ij}+\lfloor p_{ij}\rfloor )e\left[\lfloor p_{ij}\rfloor \right]$

4. Attention Calculation

   Raw:

   • $a_{ij}=\mathrm{Softmax}(q_i^T{k}_j+q_i^{T}e\left[p_{ij}\right])$

   Optimized: (Interacts with the query vector before interpolation)

   • Pre-computed for all integer positions: $z_i[p]=q_i^{T}e[p]$
   • Interpolating scalar attention contribution: $z_i\left[p_{ij}\right]=(p_{ij}-\lfloor p_{ij}\rfloor )z_i\left[\lceil p_{ij}\rceil \right]+(1-p_{ij}+\lfloor p_{ij}\rfloor )z_i\left[\lfloor p_{ij}\rfloor \right]$
   • $a_{ij}=\mathrm{Softmax}(q_i^T{k}_j+z_i\left[p_{ij}\right])$

SBA

Scaling Stick-Breaking Attention: An Efficient Implementation and In-depth Study

• Using the stick-breaking process as a replacement for softmax for attention.
• Naturally incorporating recency bias.
• No need of positional encoding.

1. Original Logits

   $$z_{ij}=\frac{q_j^T{k}_i}{\sqrt{d_{\text{head}}}}$$

2. Breakpoint Possibility

   $${\beta }_{ij}=\sigma (z_{ij})$$

3. Attention Weights

   • From $j$ to $i$ (backwards in time).
   $$A_{i,j}={\beta }_{i,j}\prod _{i<k<j}(1-{\beta }_{k,j})$$

4. Output

   $$o_j=\sum _{i=1}^{j-1}{A}_{i,j}{v}_i$$

• Numerically Stable Implementation

  By Log-Space Formulation.

  1. Sigmoid in log-space:

     $log{\beta }_{i,j}=log\sigma (z_{i,j})=z_{i,j}-log(1+exp(z_{i,j}))$

     $log(1-{\beta }_{k,j})=log(1-\sigma (z_{k,j}))=-log(1+exp(z_{k,j}))$

     Where $log(1+exp(x))$ is commonly known as softplus(x).

  2. Compute $A_{i,j}$ in log-space:

     $A_{i,j}=exp(log{\beta }_{i,j}+\sum _{k=i+1}^{j-1}log(1-{\beta }_{k,j}))$

     $A_{i,j}=exp(z_{i,j}-log(1+exp(z_{i,j}))-\sum _{k=i+1}^{j-1}log(1+exp(z_{k,j})))$

     $A_{i,j}=exp(z_{i,j}-\sum _{k=i}^{j-1}log(1+exp(z_{k,j})))$

  3. Stabilized softplus: $\mathrm{softplus}(x)=\{\begin{array}{ll}log(1+exp(x))& \text{if }x\le 15\\ x& \text{otherwise}\end{array}$

Rotary

RoPE

Roformer: Enhanced transformer with rotary position embedding

$$\underset{{\mathit{W}}_m}{\underbrace{\left(\begin{array}{ccccccc}\cos m{\theta }_1& -\sin m{\theta }_1& 0& 0& \cdots & 0& 0\\ \sin m{\theta }_1& \cos m{\theta }_1& 0& 0& \cdots & 0& 0\\ 0& 0& \cos m{\theta }_2& -\sin m{\theta }_2& \cdots & 0& 0\\ 0& 0& \sin m{\theta }_2& \cos m{\theta }_2& \cdots & 0& 0\\ ⋮& ⋮& ⋮& ⋮& \ddots & ⋮& ⋮\\ 0& 0& 0& 0& \cdots & \cos m{\theta }_{d/2}& -\sin m{\theta }_{d/2}\\ 0& 0& 0& 0& \cdots & \sin m{\theta }_{d/2}& \cos m{\theta }_{d/2}\end{array}\right)}}\left(\begin{array}{c}{q}_0\\ q_1\\ q_2\\ q_3\\ ⋮\\ q_{d-2}\\ q_{d-1}\end{array}\right)$$

where ${\theta }_i={10000}^{-2(i-1)/d}$

It works because $({\mathit{W}}_m\mathit{q}{)}^{\mathrm{\top }}({\mathit{W}}_n\mathit{k})={\mathit{q}}^{\mathrm{\top }}{\mathit{W}}_m^{\mathrm{\top }}{\mathit{W}}_n\mathit{k}={\mathit{q}}^{\mathrm{\top }}{\mathit{W}}_{n-m}\mathit{k}$

2D-RoPE

Rotary Position Embedding for Vision Transformer

$$\mathbf{R}(n,2t)=e^{i{\theta }_t{x}_n},\mathbf{R}(n,2t+1)=e^{i{\theta }_t{y}_n}$$$${\theta }_t={100}^{-t/(d_{\text{head}}/4)},\text{where}t\in \{0,1,\dots ,d_{\text{head}}/4\}$$

LieRE

LieRE: Lie Rotational Positional Encodings

• For high dimension ($n$).

• Learn skew-symmetric basis of matrices $\left\{{\mathbf{A}}_i\right\}$

  Skew-symmetric: ${\mathbf{A}}_i^{\mathrm{\top }}=-\mathbf{A}$

• For position $p$, encode as $p=\sum _{i=0}^n{p}_i{\mathbf{A}}_i$

• $\mathbf{R}(p)=\exp (\sum _{i=0}^n{p}_i{\mathbf{A}}_i)$

• $Q_i^{\prime }=\mathbf{R}(p_i)Q_i$, $K_i^{\prime }=\mathbf{R}(p_i)K_i$

ComRoPE

ComRoPE: Scalable and Robust Rotary Position Embedding Parameterized by Trainable Commuting Angle Matrices

• $f$ is a Relative Positional Encoding if and only if there is a $g$ satisfies:

  $$g(q,k,x-y)=\rho (f(q,x),f(k,y))$$

  where $\rho$ is a similarity function

• In this form, RoPE can be represented as:

  $$\{\begin{array}{l}f(q,x)={\mathbf{R}}_f(x)q\\ \rho (q,k)=q^{\mathrm{\top }}k\\ g(q,k,x-y)=q^{\mathrm{\top }}{\mathbf{R}}_f(y-x)k\end{array}$$

  which also satisfies:

  $${\mathbf{R}}_f(x{)}^{\mathrm{\top }}{\mathbf{R}}_f(y)={\mathbf{R}}_f(y-x)$$

• $\mathbf{R}$ is a rotation matrix function if

  $$\mathbf{R}(x;\{{\mathbf{A}}_1,{\mathbf{A}}_2,\dots \})=\exp (\sum _{i=1}^N{\mathbf{A}}_i{x}_i),\text{where}\exp (\mathbf{X})=\sum _{k=0}^{\mathrm{\infty }}\frac{{\mathbf{X}}^k}{k!}$$

  THEOREM:

  $${\mathbf{R}}_f(x{)}^{\mathrm{\top }}{\mathbf{R}}_f(y)={\mathbf{R}}_f(y-x)$$$$⟺\mathrm{\forall }i,j,{\mathbf{A}}_i{\mathbf{A}}_j={\mathbf{A}}_j{\mathbf{A}}_i$$

  Let ${\mathbf{A}}_i=\mathrm{diag}({\mathbf{B}}_{i1},{\mathbf{B}}_{i2},\dots ,{\mathbf{B}}_{im})$

  $$⟺\mathrm{\forall }i,j,k{\mathbf{B}}_{ik}{\mathbf{B}}_{jk}={\mathbf{B}}_{jk}{\mathbf{B}}_{ik}$$

• Then we need to find $\mathbf{B}$ that satisfies above.

  • ComRoPE-AngleMatrices:

    $${\mathbf{B}}_{ij}=\{\begin{array}{ll}{\mathbf{P}}_j-{\mathbf{P}}_j^{\mathrm{\top }},& \text{if }j\equiv i(\mathrm{mod}N)\\ \mathbf{O},& \text{otherwise}\end{array}$$

    where ${\mathbf{P}}_j$ is trainable

  • ComRoPE-LinearlyDependent:

    $${\lambda }_1{\mathbf{B}}_1={\lambda }_2{\mathbf{B}}_2=\cdots ={\lambda }_N{\mathbf{B}}_N$$

    Specially,

    $${\mathbf{B}}_i={\theta }_i(\mathbf{P}-{\mathbf{P}}^{\mathrm{\top }})$$

Method	Commutativity	Extra Parameters	Extra Time Complexity
APE	—	$nd$	$O(nd)$
Vanilla RoPE	Yes	0	$O(Lnd(bN+b^2+\frac{d}{h}))\approx O(\frac{Ln{d}^2}{h})$
LieRE	Commonly Not	$LNdb$	$O(Lnd(bN+b^2+\frac{d}{h}))$
ComRoPE-AP	Yes	$Ldb$	$O(Lnd(bN+b^2+\frac{d}{h}))$
ComRoPE-LD	Yes	$Ld(b+\frac{N}{b})$	$O(Lnd(bN+b^2+\frac{d}{h}))$

FoPE

Fourier Position Embedding: Enhancing Attention's Periodic Extension for Length Generalization

TaPE

conTextualized equivariAnt Position Embedding

Rethinking Addressing in Language Models via Contexualized Equivariant Positional Encoding

• Permutation Equivariance