Linear Attention

Original Linear Attention

The original attention mechanism is defined as:

Complexity: $\mathcal{O}(N^2{d}_k+N^2{d}_v)$

$$O=\mathrm{softmax}(Q{K}^{\mathrm{\top }})V$$

If we omit the softmax operator it becomes:

Complexity: $\mathcal{O}(N{d}_k{d}_v)$

$$O=Q{K}^{\mathrm{\top }}V=Q(K^{\mathrm{\top }}V)$$

which is of linear complexity.

In Autoagressive Models

In autoregressive models like GPT we need a causal mask:

$$\begin{array}{rl}\text{Training:}& O=\mathrm{softmax}(Q{K}^{\mathrm{\top }}\odot M)V\\ \text{Inference:}& o_t=\sum _{j=1}^t\frac{\exp (q_t^{\mathrm{\top }}{k}_j)}{\sum _{l=1}^t\exp (q_t^{\mathrm{\top }}{k}_l)}{v}_j\end{array}$$

Removing softmax yields:

$$\begin{array}{rl}\text{Training:}& O=(Q{K}^{\mathrm{\top }}\odot M)V\\ \text{Inference:}& o_t=\sum _{j=1}^t(q_t^{\mathrm{\top }}{k}_j)v_j\end{array}$$

Unfortunately the Hadamard product ($\odot$) does not commute with matrix multiplication, so the operation remains quadratic.

RNN-like Sequential Form

Even though, Transformers are RNNs: Fast Autoregressive Transformers with Linear Attention observes that the inference equation can be written in an RNN-like form:

$$o_t=\sum _{j=1}^t(v_j{k}_j^{\mathrm{\top }})q_t=S_t{q}_t,S_t=S_{t-1}+v_t{k}_t^{\mathrm{\top }}$$

This achieves linear time, but introduces two drawbacks:

1. Memory during autograd:

   High memory footprint during autograd: every intermediate state $S_t$ must be stored, resulting in $\mathcal{O}(L{d}^2)$ memory usage. The authors alleviate this by recomputing $S_t$ on-the-fly during back-propagation.

2. Parallelism:

   Poor training parallelism: the update is element-wise instead of large matrix multiplications, which under-utilizes GPU tensor cores.

   A compromise is the chunkwise algorithm proposed in Transformer Quality in Linear Time, which allows parallelism while remaining linear.

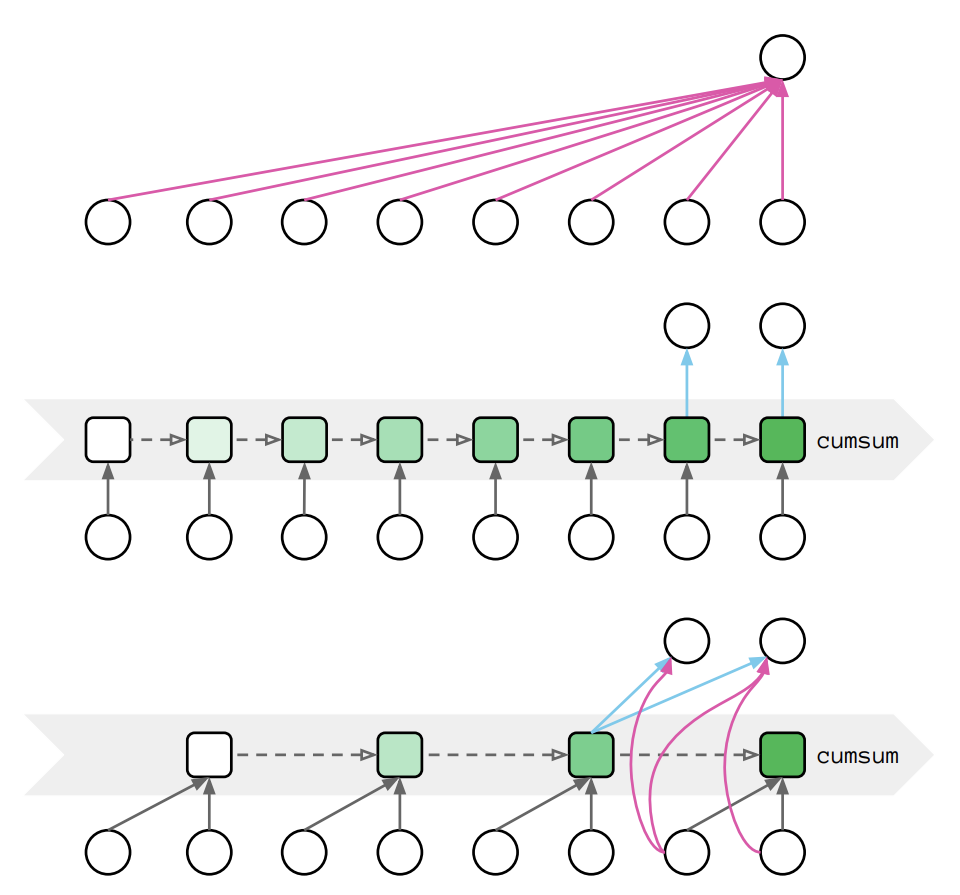
   From up to bottom: Parallel form, recurrent form, chunkwise parallel form:

Gated Linear Attention

A learnable 2D forget gate $G_t\in (0,1{)}^{d_k\times d_v}$ is added:

$$S_t=G_t\odot S_{t-1}+k_t^{\mathrm{\top }}{v}_t$$

This is very general and encompasses many recent RNNs with 2D hidden states:

Gated Linear Attention Transformers with Hardware-Efficient Training also proposed its GLA:

• Recurrent form:

$$S_t=({\alpha }_t^{\mathrm{\top }}1)\odot S_{t-1}+k_t^{\mathrm{\top }}{v}_t=\mathrm{Diag}({\alpha }_t)S_{t-1}+k_t^{\mathrm{\top }}{v}_t$$

• Parallel form:

$$S_t=\sum _{i=1}^t(\left(\prod _{j=i+1}^t{\alpha }_j\right)\odot k_i^{\mathrm{\top }}{v}_i)$$

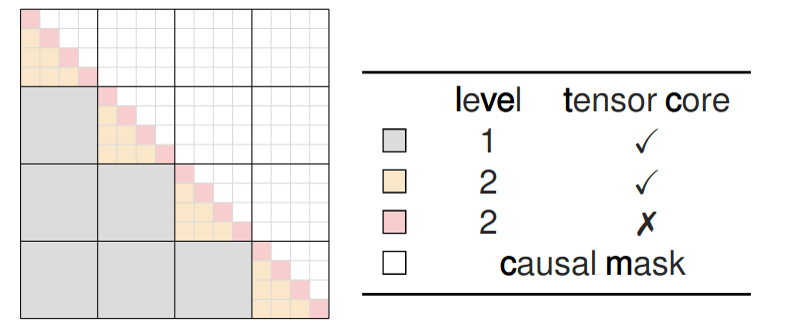
• Chunkwise parallel:

  

References

Sonta. "Zhihu answer." https://www.zhihu.com/question/9740764576/answer/80735153803

Katharopoulos A., Vyas A., Pappas N., Fleuret F. "Transformers are RNNs: Fast Autoregressive Transformers with Linear Attention." https://arxiv.org/abs/2006.16236

Vyas A., Katharopoulos A., Fleuret F. "Transformer Quality in Linear Time." https://arxiv.org/abs/2202.10447

Yang S.L., Wang B.L., et al. "Gated Linear Attention Transformers with Hardware-Efficient Training." https://arxiv.org/abs/2312.06635